TW / MMACTF2016 Crypto180 「ESPer」を解いてみた

チームの勉強会で，MMACTF 2016 で出題された「ESPer」という問題を扱いました．チームメンバーが発表をしてくれたのですが，より理解を深めるため復習もかねてアプローチや解法を書いてみます．本番で解いた問題のWrite-upではありません．

最後にまとめとして解法の流れを書いています．

MMACTF 2016

正確には，Tokyo Westerns / MMA CTF 2nd 2016 です．今年は 9/3 9:00 – 9/5 9:00 の開催でした．諸事情によりほとんど参加できず，ppcのwarm upのフラグ1くらいしか送ってません :(

暗号問題がたくさん出題されていたようなので，本番で解けなかったことが悔やまれます…

Crypto180 「ESPer」

名前からエスパー感が出ていますがエスパー問題ではありません．個人的には面白い問題だと感じました．（こういう簡単すぎず，難しすぎずという問題を作れるのすごい…）

まずは問題を見てみます．

問題文

エスパーですか?

nc cry1.chal.ctf.westerns.tokyo 37992

アプローチ

非常にシンプルな問題文．私はエスパーではありませんがnetcatでアクセスしてみます．すると以下のような文面が送られてきます．

これはnetcatでアクセスする問題によくある前哨戦です．「ある条件を満たす文字列を送ることができたら，肝心の問題を見せてやるよｗ」みたいな感じです．

この問題では，「指定した範囲のバカでかい数値の中でも，SHA1ハッシュを取ると上位5桁が00000になるような数値を送れ」と言っているようです．思考停止で総当たりします．

ここで求められたnumberをsendすれば，肝心の問題が提示されるはずです．ここではrecvで受け取るのではなく，telnetlibモジュールにあるinteractを用いて，途中からインタラクティブな操作に戻してみます．この方が試行錯誤がしやすいです．

すると以下のようになります．

 

ここからが本番です．答えを送ると，何やらRSAの鍵を生成しているのが分かります（ちなみにですが，RSA鍵はnetcatの度に生成されます，しかしeの値は一般的な65537に固定されていますので，公開鍵で毎回変化するのはnの方のみです．）．その後1~4の選択肢が出てきます．これらはそれぞれ以下のようなことをしてくれます．

1. 生成した公開鍵を利用して，送った平文(十進数値)を暗号化してくれる．
2. 生成した秘密鍵を利用して，送った暗号文(十進数値)を復号してくれる．
3. 問題の詳細を教えてくれる．
4. Flagを公開鍵で暗号化した値(十進数値)が送られてきて接続が終了する．

4をchoiceするとフラグの暗号文が送られてくることから，何とかして秘密鍵の値を求めて復号する問題かなという予想をします．定石としては，公開鍵nは分かっている状態で，秘密鍵dの値を求めたい->二つの素数p,qを何とかして特定する，という流れですよね．

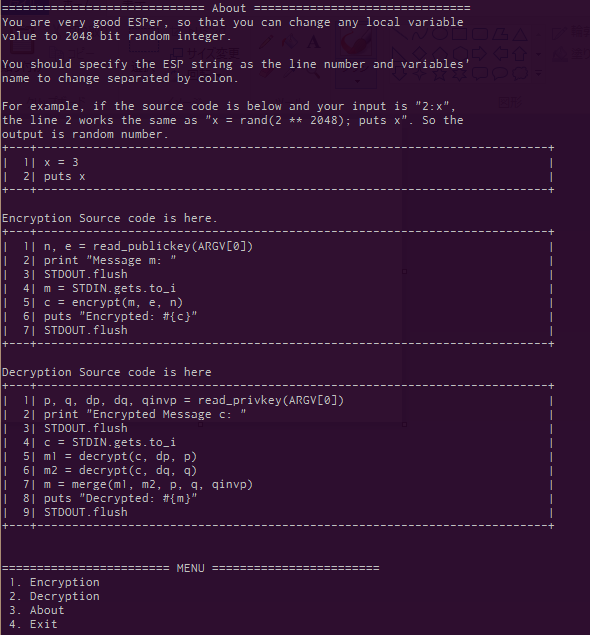
何はともあれ，3のAboutを見てみます．

 

「お前はすごいエスパーだから，どれか一つのローカル変数の値を適当な値に書き換えられるよ．」

私はエスパーだったようです．

暗号化や復号の処理を行う際，その処理で使われている変数の中身を一つだけランダムな値に変えることができます．

1,2を選択すると，送信する平文(暗号文)を聞かれる前に，どの変数をぶち壊したいか聞かれます．求められたフォーマットでない文字を入力すると，invalidとなり，変数を破壊せず通常の処理が行われます．通常の処理というのが，画像中段あたりに書いてあるものになります．RSAにおける暗号化・復号の一般的な処理と大差ないと思います．が，少し癖があるのは復号処理です．

RSAの暗号化・復号の処理と言えば，C = M^e mod n , M = C^d mod n を想像すると思います．しかし秘密鍵dの値は非常に大きいので，復号の際にC^dを計算するのに比較的時間がかかってしまいます（eの値は65537固定であることが多く，2進数にした時のために工夫された値なので，暗号化はバイナリ法かなにかで簡単に計算できたと思います）．そこで復号には別の方法として，中国の剰余定理(CRT : Chinese Remainder Theorem)を使った計算方法があります．この問題の復号処理はおそらくそれを使っています．

今回の問題の条件はこうです．

1. 好きな値の暗号化結果が分かる
2. 好きな値の復号結果が分かる
3. 暗号化・復号処理のうち好きな変数を適当な値（乱数）に書き換えられる
4. Flagの暗号文はわかる

これらの情報から何とかして秘密鍵dを求められないか，考えてみます．

公開鍵nは何？

この手の問題は大抵公開鍵(n,e)は明かされていることが多い（気がするの）ですが，今回はnがわかっていません．しかしこの問題でnを求めるのは簡単です．上述したように，暗号化は平文をmとした時，

[math]c = m^e\; mod \;n \tag{a}[/math]

で計算されます．この書き方を少し変えると，

[math]m^e = \alpha\;n+ c \tag{b}[/math]

と表せます．これを踏まえた上で，例えば2,3という数値を暗号化した時，式(b)はそれぞれ，

[math]2^e = \alpha\;n+ c\tag{c}[/math]

[math]3^e = \beta\;n+ c \tag{d}[/math]

となります．少し変形して，

[math]2^e-c = \alpha\;n\tag{e}[/math]

[math]3^e-c = \beta\;n\tag{f}[/math]

ですね．ということは，この二つの数字のgcd(最大公約数)を取れば，nの値がわかりそうです．実際にわかります．

素数p,qを求めたい

一般的に秘密鍵dを求めるためには，p,qを求める必要があります（攻撃によってはp,qが分からずとも直接dを求めてしまうものもありますが）．そのためにまずは，1の暗号化処理と2の復号処理のどの変数を壊すと，結果として送られてくる値にどのような変化が起こるのか考えてみます．

1の暗号化処理の変数を壊す？

まずは暗号化処理について考えてみます．暗号化の処理はおそらく単純にC = M^e (mod n) をしているだけかと思われます．破壊できる変数は[math]n,e,m,c[/math]です．mはこちらから送る平文ですし，暗号文は最後に送られてくる値なので，破壊しても意味がなさそうです．かと言ってnとeを破壊しても，暗号文が変化するだけであまり有用な結果は得られなさそうです．

2の復号処理の変数を壊す

こちらで使われている変数は，[math]p,q,dp,dq,q\;inv\;p,c,m_1,m_2,m[/math]の9つがあり，壊しがいがありそうです（壊せるのは一つですが）．

どの変数を壊すと何が起きるか，RSAの復号処理の式をノートに書きながら色々考えます．そのためにCRTを用いたRSAの復号処理を簡単に振り返ってみます．

CRTを使った復号処理（証明などは割愛）

復号処理をするには，以下の[math]m_1，m_2[/math]を計算する必要があります．

[math]m_1=c^{\;d\;mod\;(p-1)}\;(mod\; p)\tag{1}[/math]

[math]m_2=c^{\;d\;mod\;(q-1)}\;(mod\; q)\tag{2}[/math]

これらについて，今回の変数に置き換えてみます．

[math]m_1=c^{\;dp}\;(mod\; p)\tag{3}[/math]

[math]m_2=c^{\;dq}\;(mod\; q)\tag{4}[/math]

[math]dp,dq[/math]は，1行目のread_privkey(ARGV[0])の部分で作られています．秘密鍵には[math]d\;mod\;(p-1), d\;mod\;(q-1)[/math]の値が入っているので，[math]dp,dq[/math]にこれが入ることが予想できます．それぞれExponent1,Exponent2という名前で秘密鍵に含まれます．同様にCoefficientという値も入っています．こちらは[math]q^{-1}\;mod\;p[/math]の計算結果で，こちらもCRTで復号処理を行う時に使用します．

ここで，やっとCRTについてです．CRT(中国の剰余定理)とは，

a，b を互いに素な正整数（即ち最大公約数が１）とする。x，y を整数とする。 このとき，

[math]m\equiv x\;(mod\;a)\tag{5} [/math]

[math]m\equiv y\;(mod\;b) \tag{6}[/math]

を満たす整数 m が [math]ab[/math] を法にして唯ひとつ存在する。

といった定理です(参考:中国の剰余定理)．

式(3),(4)の右辺に注目します.[math]p,q[/math]は，それぞれ素数であるため互いに素です．そして，[math]c^{dp},c^{dq}[/math]は整数です．すなわち，

[math]m\equiv c^{dp}\;(mod\;p)\tag{7} [/math]

[math]m\equiv c^{dq}\;(mod\;q)\tag{8}[/math]

となるような[math]m[/math]が[math]p*q[/math]を法として存在します．RSAの復号処理において，この[math]m[/math]が平文mとなります．

 

式(7),(8)は，式(3),(4)より以下のようにも書けますね．

[math]m\equiv m_1\;(mod\;p)\tag{9} [/math]

[math]m\equiv m_2\;(mod\;q)\tag{10}[/math]

だからどうした

それぞれの変数の関係性がわかりました．肝心なのはどの変数を壊せばよいのかという問題ですが，答えは「[math]m_1,m_2,dp,dq[/math]のどれか一つさえ壊せば良い」です．というよりは，最終的に破壊しなければいけないのは[math]m_1,m_2[/math]のどちらかなのですが，[math]dp,dq[/math]を破壊すると結果的にそれぞれが破壊されるので，その4つのうちどれかということになります．

では，[math]m_2[/math]を破壊してみることにします．[math]m_2[/math]を破壊すると，式(9),式(10)は以下のような関係に変化します．

[math]m’\equiv m_1\;(mod\;p)\tag{11} [/math]

[math]m’\equiv m’_2\;(mod\;q)\tag{12}[/math]

 ダッシュ(‘)が付いているものが壊れた値です．[math]m_2[/math]が破壊されているので，破壊された[math]m_2[/math]を使って復号した結果である[math]m[/math]も破壊されおかしな値になります．ここで，[math]m_2[/math]を破壊しなかった時の式(10)と，破壊した時の式(12)を比較したいのですが，ちょっと書き方を変えてみます．

[math]m= \alpha\; q + m_2\tag{13} [/math]

[math]m’= \alpha\;’\; q + m_2\tag{14} [/math]

このように書けますよね．この2つの式を見ると，なんだか引き算をしたくなってきます．式(14)-式(13)をすると，

[math]m’-m= (\alpha\;’-\alpha) q\tag{15} [/math]

おや，通常の復号処理により得た[math]m[/math]と，変数破壊を行った[math]m'[/math]を得て引き算を行うと，その値は[math]q[/math]の倍数になっているようです．ここで，先に手に入れておいた[math]n=p×q[/math]であるため，[math]n[/math]も[math]q[/math]の倍数です．つまり，[math]m’-m[/math]と[math]n[/math]のgcdを取れば，[math]q[/math]がわかりそうです．そして，[math]n/q[/math]をすれば[math]p[/math]が分かってしまいそうです．

勝ち確です

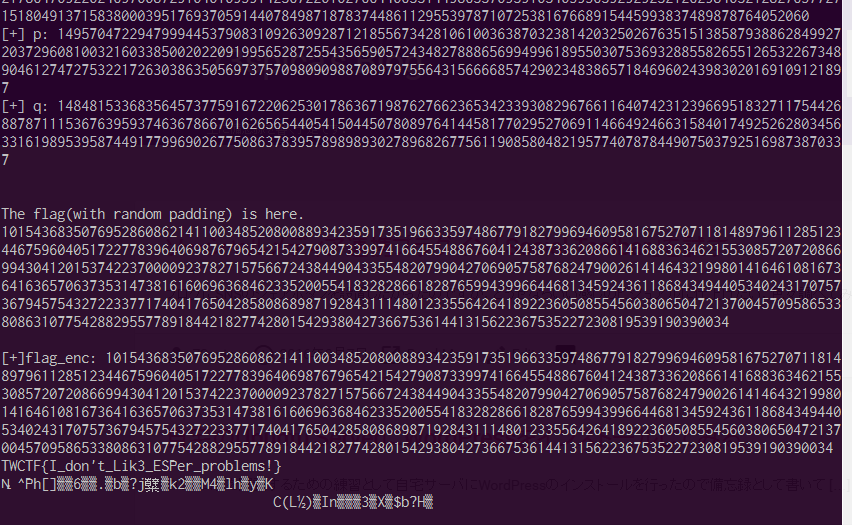
[math]p,q[/math]の値がわかったので，秘密鍵[math]d[/math]を計算します．秘密鍵の計算過程は省略いたします．最後に4.Exitをした際，そのセッションで作られた公開鍵によって暗号化されたFlagが送られてくるので，それを生成した秘密鍵で復号すればフラグを得ることができます．

 

TWCTF{I_don’t_lik3_ESPer_problems!}

まとめ

Crypto180「ESPer」の解法の流れは以下になります．

1. 公開鍵nの値を求める
2. [math]m_2[/math]をぶっ壊して得た[math]m'[/math]と,通常処理で得た[math]m[/math],また公開鍵nからpを得る
3. [math]n/p[/math]より[math]q[/math]を得る
4. 秘密鍵を求める
5. フラグを復号する

この中でも，2の部分の攻撃手法をRSA-CRT fault attack   と呼ぶそうです

分かってしまえば…という感じですが，本番中だと中々思いつかないものです．精進したいと思います．

また中国の剰余定理についてはとてもわかりやすい説明のあるサイトを参考として載せておきます．

余談

暗号問題は頭がこんがらがります…．もしおかしな点があったらご指摘いただけたら幸いです．

あと，ppcのwarm upのフラグ1って，確率的に何もしなくてもフラグが降ってきますよね…

何も解いてないのと同義で悲しみです．

参考

• ₍₍ (ง ˘ω˘ )ว ⁾⁾ < 暗号楽しいです | 数学 – 中国人剰余定理
• 公開鍵暗号：RSA暗号