「ESPer」に引き続き,「Vigenere Cipher」も解いてみました.
またまたチームの勉強会で扱ったものです.
Crypto200 「Vigenere Cipher」
ヴィジュネル暗号の問題みたいです.
早速問題を見てみます.
問題文
vigenere.7z
アプローチ
上記の7zipのファイルが渡されるのみです.解凍すると以下の3つのファイルが出てきます.
- README
- encrypted.txt
- cipher.py
まずは読めと言われているのでREADMEを見てみます.
|
1 2 3 |
$ file plain.txt plain.txt: ASCII text $ python cipher.py encrypt key plain.txt > encrypted.txt |
と,いう内容がファイルに書かれています.cipher.pyの使い方のようですね.ASCIIで書かれたテキストファイル「plain.txt」を読み込んで,鍵keyを使って暗号化(encrypt)しているようです.その結果をencrypted.txtに書き出しています.encrypted.txtは渡されたファイル群にありました.そちらも見てみます.
|
1 |
a7TFeCShtf94+t5quSA5ZBn4+3tqLTl0EvoMsNxeeCm50Xoet+1fvy821r6Fe4fpeAw1ZB+as3Tphe8xZXQ/s3tbJy8BDzX4vN5svYqIZ96rt35dKuz0DfCPf4nfKe300fM9utiauTe5tgs5utLpLTh0FzYx0O1sJYKgJvul0OfiuTl00BCks+aaJZm8Kwb4u+LtLCqbZ96lv3bieCahtegx+7nzqyO6YCb4b9LovCELZ9Pe0L5rLSaBDzXaftxseAw1JzCF0MGjeCacKb69u9TlgCudZT6Os3ojhcWxD914vNHfeCuaJvH4s4aarBKlGdsT8G4UKZhfJB+y0LbjqCOnZT6baF1WiZeNtfsNtuoo+c== |
暗号文なのでわけが分かりませんが,base64エンコードされていることが分かります.詳細はcipher.pyを見てみます.Python3を使っているようですね.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# Python 3 Source Code from base64 import b64encode, b64decode import sys import os import random chars = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/' def shift(char, key, rev = False): if not char in chars: return char if rev: return chars[(chars.index(char) - chars.index(key)) % len(chars)] else: return chars[(chars.index(char) + chars.index(key)) % len(chars)] def encrypt(message, key): encrypted = b64encode(message.encode('ascii')).decode('ascii') return ''.join([shift(encrypted[i], key[i % len(key)]) for i in range(len(encrypted))]) def decrypt(encrypted, key): encrypted = ''.join([shift(encrypted[i], key[i % len(key)], True) for i in range(len(encrypted))]) return b64decode(encrypted.encode('ascii')).decode('ascii') def generate_random_key(length = 5): return ''.join(map(lambda a : chars[a % len(chars)], os.urandom(length))) if len(sys.argv) == 4 and sys.argv[1] == 'encrypt': f = open(sys.argv[3]) plain = f.read() f.close() key = generate_random_key(random.randint(5,14)) print(encrypt(plain, key)) f = open(sys.argv[2], 'w') f.write(key) f.close() elif len(sys.argv) == 4 and sys.argv[1] == 'decrypt': f = open(sys.argv[3]) encrypted = f.read() f.close() f = open(sys.argv[2]) key = f.read() f.close() print(decrypt(encrypted, key), end = '') else: print("Usage: python %s encrypt|decrypt (key-file) (input-file)" % sys.argv[0]) |
encrypted.txtを見て,てっきり暗号文をBase64しているのかと思いきや,平文をBase64した後にヴィジュネル暗号の換字をしているみたいです.
ポイントは以下になります.
- 暗号化モードと復号モードがある
- 問題名の通り,暗号方式はヴィジュネル暗号っぽい
- 鍵長は5~14でランダム
- shift関数で換字している
ここで,ヴィジュネル暗号について考えるための周辺知識を振り返ってみます.
古典暗号
現代暗号である共通鍵暗号(AES, DES)や公開鍵暗号(RSA)とは異なり,1970年代以前から使われていたような暗号を古典暗号と言います(DESが出てきたのが1977年くらい).有名な古典暗号としては,シーザー暗号やヴィジュネル暗号があります.また,大きく分けて以下の二つの暗号に分けられます.
- 換字式暗号
- 転置式暗号
今回の問題で扱われているヴィジュネル暗号は換字式暗号にあたります.
古典暗号と現代暗号の違い
古典暗号と現代暗号の違いとして,安全性の担保の方法が異なります.
古典暗号は暗号アルゴリズムを隠すことで安全性を担保します.例えば,「この暗号はシーザー暗号だ!」とばれてしまうと,いくつずらすかなどのルールが分からなくても,総当たりでたちまち解読されてしまいます.ヴィジュネル暗号に関しても,現代知られている解読法と高いマシンスペックによって解読することが可能です.
それに対して現代暗号は,暗号化に使用された鍵さえ秘匿にしていれば,暗号アルゴリズムは公開して良いという強気な暗号です.というのも,コンペ等で仕様を決めるため,様々な暗号研究者によって強度をテストされています.そこで計算量的安全性(RSA)や情報量的安全性(バーナム暗号)というのが証明されているのです.鍵って何ぞやという詳しい話については今回は割愛いたします.
ヴィジュネル暗号とは
ヴィジュネル暗号は古典暗号の一種です.その中でも換字式暗号に分類されます.ヴィジュネル暗号は,ヴィジュネル方陣と呼ばれる変換表と,鍵を用いた文字の変換を行います(これが換字です).詳細な暗号化方式はwikipediaの説明が分かりやすいと思います.
今回の問題のヴィジュネル暗号
ヴィジュネル暗号について振り返ったところで,cipher.pyを振り返ります.wikipediaのヴィジュネル暗号では,ヴィジュネル方陣を用いて換字を行っていたところを,本問題ではshiftという関数で換字を行っています.
具体的には,まず平文の1文字目と鍵の1文字目に注目します.平文の1文字目が変数charsの文字群の中で,何番目に存在するか(要はindex)を確認します(chars.index(char)).次に鍵の1文字目が変数charsの文字群の中で,何番目に存在するか(index)を確認します(chars.index(key)).
それらを足し合わせた数値のindexにあるcharsの文字を換字の結果として返します.足し合わせた際に,charsの長さを超えてしまう場合が考えられるので,len(chars)で割った余りを取ることでcharsの範囲内に収めます.
これを平文2文字目+鍵2文字目,平文3文字目+鍵3文字目,…と繰り返して平文が終わるまで行います.なお,鍵長は最大でも14文字であり,これを超える場合は再び鍵の1文字目から同じ動作を繰り返します.
これらの動作は,適当な文字列をshift関数に投げれば容易に確かめることができます.
ヴィジュネル暗号の解読法
ヴィジュネル暗号の解読法の一つに,カシスキー・テスト(Kasiski examination)というものがあります.
またまたWikipediaの引用で申し訳ありません(Wikipedia先生は偉大です).説明にあるように,カシスキー・テストはある程度長い暗号文でないと使えません.また,その暗号がヴィジュネル暗号であることを知っていることが前提の解読法になります.
カシスキー・テストの手順は,大きく分けて以下の二つに分かれます.
- 鍵長を推測する
- 頻度分析を用いて鍵を推定する
結論から言うと,1.の鍵長の推定は可能ですが,2.の頻度分析を用いた鍵の推定はできません.理由は平文が一般的な英文ではないためです.
頻度分析は,各アルファベットが,英文中にどのような頻度で出現するかということをあらかじめ調べておきます.そして,換字式暗号中に出現するアルファベットの頻度を分析し,それらの頻度を比較することで推定を行います.しかし今回の平文は,暗号化前jに一度base64エンコードされています.この時点で,各文字の出現頻度はほぼ均一になると考えられます.ですから,今回は2.の手順で鍵を推定することができないということになります.
ともあれ,鍵長が分からなければ鍵の推定も難しいと考えられますので,カシスキー・テストの鍵長推測の方法を見ていきます.
カシスキー・テストによる鍵長の推測
鍵長の推測については,wikipediaに加えて以下のサイトが分かりやすかったです.
要は,暗号文中に何回も出てくる文字列を見つけ,その間隔を調べれば良いです.そして全ての間隔に共通の因数が鍵長の候補になります.それらの処理を私はpythonのfindやらスライスを使って書きましたが,もっと良い方法がある気もします.
今回の問題の暗号文について上記の処理を行うと,鍵長は6文字か12文字と推定できます.結論から言うと,正しい鍵長は12文字です.この後の処理で鍵の推定を行いますが,鍵長を6文字として実行すると上手くいきません.
鍵の推定
鍵長が12文字であると分かりました.しかし総当たりをするには12文字は長すぎます(64^12 = 4722366482869645213696通り).かといって今回は頻度分析による鍵長の推定ができません.平文を暗号化する前にBase64エンコードを行っているためです.
何とかして今回の問題において,現実的な時間で鍵を特定する方法を見つける必要があります.そのために今回の問題の暗号化の仕様を詳しく見てみます.
Base64とは
Base64の仕様を見てみます.
上記を参照すると,Base64エンコードの際は,
- 1文字8bitで表現される元データを6bitごとに分割
- 各ビット6bitを1文字に変換.4文字を1ブロックとして変換し,4文字に満たない場合は=でパディング
という処理を行います.このことから,平文の3文字( 8bit * 3文字 = 24bit)が,4文字( 6bit * 4文字 = 24bit)に変換されていることが分かります.実際に試すと以下のようになります.
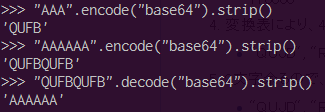
“AAA”という3文字が”QUFB”という4文字に変換されていることが分かります.また,それは何文字になっても同じことです.
逆変換する場合も同様です.”QUFBaaaa”という文字列を逆変換すると”QUFB”の部分はきちんと”AAA”と変換されています.適当に入力した部分である”aaaa”は,先頭部分はたまたまASCII範囲内に変換されていますが,後半はASCII範囲外です.QUFBの一部を変化させた部分は,”QU”が正しいので1文字目のAは正しく逆変換されて,後半はやはり変換に失敗しています.
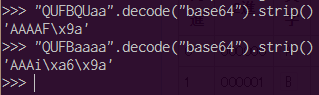
つまりBase64には,一部が間違っていても,正しい部分はきちんと逆変換し読むことができるという特徴があります.
cipher.pyの暗号化・復号処理を再考する
説明のために,以下のような文章を暗号化してみます.文章の部分はWikipdiaのヴィジュネル暗号の冒頭です.
|
1 |
The Vigenere cipher is a method of encrypting alphabetic text by using a series of different Caesar ciphers based on the letters of a keyword. It is a simple form of polyalphabetic substitution.TWCTF{This_is_test} |
(勉強会用に試したものなので,フラグ形式を知っている上で末尾にテスト用のフラグを付けていますが説明には関係ないので気にしないでください.)
この平文をcipher.pyで暗号化すると以下のようになります.
|
1 |
XyZa9rA06ncl1Ppa9so0j3AceaheDkcSP3icfyZkooc66FUcdetnFJczhhmeKylhDsUS5JcRcOs7EswDkZU/gKhQDOY56VU+KztaD+YWjVUm1ah/BIAX6i2cdfw7fOgWjnYpKyteDsUWjK590elooIrRinl9fyZa9s+Wk4+cefs7COzR5dUi1P3SCPkVSFUAfuheDkcSP46gdPhhoEcXio2kKyPb9tc6i4E+dzhdnIkWk3EaKztQn/ozhi+Sfy3kC6Gt2l6LTf/JBsY+4nEqZVxaDPsI |
この時の鍵は,c4S1BYNLhxt3(12桁)でした.
この暗号文を例にして考えてみます.これを適当な鍵”aaaaaaaaaaaa”でdecryptしてみます.decryptは,cipher.pyのdecrypt関数を使います.
|
1 |
_&Z\xf6\xb04\xeaw%\xd4\xfaZ\xf6\xca4\x8fp\x1cy\xa8^\x0eG\x12?x\x9c\x7f&d\xa2\x87:\xe8U\x1cu\xebg\x14\x973\x86\x19\x9e+)a\x0e\xc5\x12\xe4\x97\x11p\xeb;\x12\xcc\x03\x91\x95?\x80\xa8P\x0c\xe69\xe9U>+;Z\x0f\xe6\x16\x8dU&\xd5\xa8\x7f\x04\x80\x17\xea-\x9cu\xfc;|\xe8\x16\x8ev)++^\x0e\xc5\x16\x8c\xae}\............ |
こんな感じになります.異なる鍵で復号した結果であるめちゃくちゃな base64コードをデコードするので,デコード結果がASCII範囲内にならず読むことができません.
では,一部正解の鍵”c4S1aaaaaaaa”でdecryptするとどうなるでしょうか.ここからは勉強会の時に使った資料も使ってみます(説明って難しい).
ところどころ読める文字が現れているのが分かります.それも一定間隔で読める部分が現れています(9文字間隔).これは,ヴィジュネル暗号とBase64を用いた暗号化・復号であるために現れる特徴です.Base64は一部が正しければきちんとデコードされます.ヴィジュネル暗号は鍵を使いまわすので,鍵の一部が正しければ,正しい部分は一定間隔で復号に成功します.
上の例において鍵の正しい部分は12文字の内の先頭4文字です.ということは,正しく復号される部分は,暗号文を12文字ずつに区切ったうち先頭4文字です.
Base64は,平文3文字を4文字に変換するのでした.そのtめ,デコード時は4文字が平文3文字にデコードされます.
鍵推定
つまり今回の暗号方式では以下の鍵推定が可能になります.
- 12文字の鍵を4文字*3ブロックに分ける
- 4文字を総当たり (64^4 =16777216通り )
- もしも鍵が正しければ,鍵の正しい部分でdecryptされうる部分は全てASCII範囲内に変換される.そうでないならその鍵の4文字は正しくない
- 次の鍵ブロックについて2~4を繰り返す.3ブロックやったら終了
Base64を噛ませていないただのヴィジュネル暗号では,全てASCII範囲内にはなるのでこのような判定はできません.しかし,Base64を噛ませていると,このような判定が可能なのです.もちろん正しい鍵に近い4文字の時,偶然全てがASCII範囲内になることもあるので,一意には定まりません.あくまで推定です.
あとはこの処理を行うプログラムを書けば良いです.
※鍵と暗号文は,1ブロック4文字で12文字周期なのですが,平文では1ブロック3文字で9文字周期になります.頭がこんがらがります.
鍵推定処理の高速化
上の処理のままでも,時間をかければ答えは求められると思います.しかし,以下のサイトの方(うさぎさん)はもっと総当たり空間を狭くする方法を取っており,それを参考にさせていただきました.
例えば,以下のような場合を考えます.
まず,3分割した鍵の1ブロック目(4文字)の2文字だけが正しい場合は以下のようになります.

平文1ブロック1文字目は正しく復号されます.
では次に,3文字だけが正しい場合は以下のようになります.
平文1ブロック2文字目までは正しく復号されています.
つまり,1ブロックの前半が正しければ,暗号文の前半部分もきちんと復号されます.
- 鍵が2文字正しければ1文字見える
- 鍵が3文字正しければ2文字見える
- 鍵が4文字正しければ3文字見える
何が言いたいかと言いますと,例えば鍵の1ブロックが”b4aa”である鍵を試している時,この時点で既にこの鍵で復号されるはずの1文字がASCII範囲内でなければ,それ以降の”b4ab”などは確認する必要が無い(“b5aa”に行ってよい)ということになります.
カシスキー・テストと鍵推定の実装
これらを実装したコードが以下になります.is_asciiの部分がASCIIの判定ですが,当初言葉通りの意味でのASCII範囲内にすると候補が膨大になってしまいました.かといって,以下の表で言うSPACEである32(10進数)からチルダ(~)である126までを範囲とすると候補が無くなりました.
良く見ると10が改行なので,改行くらいは入るかなと思い,「32以下で10の改行だけは許す」としたらかなり絞れました.あとは最後にフラグ形式っぽい文字列のもの(“TWCTF{“を含むもの)だけ表示するとすると,鍵候補を6つまで絞り込めます.ここまで来れば実際に読んで答えが分かると思います.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
# Python 3 Source Code from base64 import b64encode, b64decode import sys import os import random from fractions import gcd from math import sqrt candi_count = 0 chars = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/' encrypted = "a7TFeCShtf94+t5quSA5ZBn4+3tqLTl0EvoMsNxeeCm50Xoet+1fvy821r6Fe4fpeAw1ZB+as3Tphe8xZXQ/s3tbJy8BDzX4vN5svYqIZ96rt35dKuz0DfCPf4nfKe300fM9utiauTe5tgs5utLpLTh0FzYx0O1sJYKgJvul0OfiuTl00BCks+aaJZm8Kwb4u+LtLCqbZ96lv3bieCahtegx+7nzqyO6YCb4b9LovCELZ9Pe0L5rLSaBDzXaftxseAw1JzCF0MGjeCacKb69u9TlgCudZT6Os3ojhcWxD914vNHfeCuaJvH4s4aarBKlGdsT8G4UKZhfJB+y0LbjqCOnZT6baF1WiZeNtfsNtuoo+c==" def shift(char, key, rev = False): if not char in chars: return char if rev: return chars[(chars.index(char) - chars.index(key)) % len(chars)] else: print((chars.index(char) + chars.index(key)) % len(chars)) return chars[(chars.index(char) + chars.index(key)) % len(chars)] def encrypt(message, key): encrypted = b64encode(message.encode('ascii')).decode('ascii') return ''.join([shift(encrypted[i], key[i % len(key)]) for i in range(len(encrypted))]) def original_decrypt(encrypted, key): encrypted = ''.join([shift(encrypted[i], key[i % len(key)], True) for i in range(len(encrypted))]) return b64decode(encrypted.encode('ascii')).decode('ascii') # not using encode or decode ascii def decrypt(encrypted, key): encrypted = ''.join([shift(encrypted[i], key[i % len(key)], True) for i in range(len(encrypted))]) return b64decode(encrypted) def generate_random_key(length = 5): return ''.join(map(lambda a : chars[a % len(chars)], os.urandom(length))) def Kasiski_exam(encrypted): strlist = [] count = 0 indexlist = [] for i in range(len(encrypted)): for j in range(i,len(encrypted)): if j-i<3: continue start = i search_str = encrypted[i:j] while True: detect = encrypted[start:].find(search_str) if detect == -1: break else: count+=1 if count==2: strlist.append(search_str) indexlist.append(detect+j-i) start += detect+(j-i) if count==0: break count=0 print(indexlist) print(strlist) anslist = my_factor(indexlist) return anslist def my_factor(numlist): factor_list = [] for x in range(2,int(sqrt(numlist[0]))+1): if numlist[0]%x == 0 and x>=5 and x<=14: factor_list.append(x) for i in range(1,len(numlist)): anslist = list(factor_list) num = numlist[i] for x in factor_list: if num%x !=0: anslist.remove(x) return anslist def is_ascii(string): if string: for char in string: if char > 126: return False if char<32 and not char==10: return False return True def split_str_and_isascii(plain,num,block): start = 3*block for i in range(start,len(plain),9): if not is_ascii(plain[i:i+num]): return False return True # if key_len == 12 def brute_key(encrypted,key_len): global candi_count candi_key_list = [[],[],[]] for block in range(int(key_len/4)): for a in chars: for b in chars: if not split_str_and_isascii(decrypt(encrypted,a+b+"aa"),1,block): continue for c in chars: if not split_str_and_isascii(decrypt(encrypted,a+b+c+"a"),2,block): continue for d in chars: if split_str_and_isascii(decrypt(encrypted,a+b+c+d),3,block): candi_key_list[block].append(a+b+c+d) candi_count+=1 return candi_key_list #if key_len == 6 def brute_key_6(encrypted,key_len): global candi_count candi_key_list = [] for block in range(int(key_len/4)): for a in chars: for b in chars: if not split_str_and_isascii(decrypt(encrypted,a+b+"aa"),1,block): continue for c in chars: if not split_str_and_isascii(decrypt(encrypted,a+b+c+"a"),2,block): continue for d in chars: if split_str_and_isascii(decrypt(encrypted,a+b+c+d),3,block): candi_key_list.append(a+b+c+d) candi_count+=1 return candi_key_list def main(): # ==== kasiski examination ==== factor_list = Kasiski_exam(encrypted) # [6,12] key_len = factor_list[1] # ==== brute force attack to base64 ==== print("Start brute force...") candi_key1,candi_key2,candi_key3 = brute_key(encrypted,key_len) print(candi_key1) print(candi_key2) print(candi_key3) # ==== key candidate ==== keylist = [] return for key1 in candi_key1: for key2 in candi_key2: for key3 in candi_key3: keylist.append(key1+key2+key3) print(candi_count) print(keylist) # if "TWCTF{" in decrypted, It is highly possible that the key is correct. for key in keylist: dec = decrypt(encrypted,key) check = b"TWCTF{" if check in dec: print("--------- key candidate : decrypted ---------------") print(key,":",dec) print() if __name__ == '__main__': main() |
以下,実行結果です.
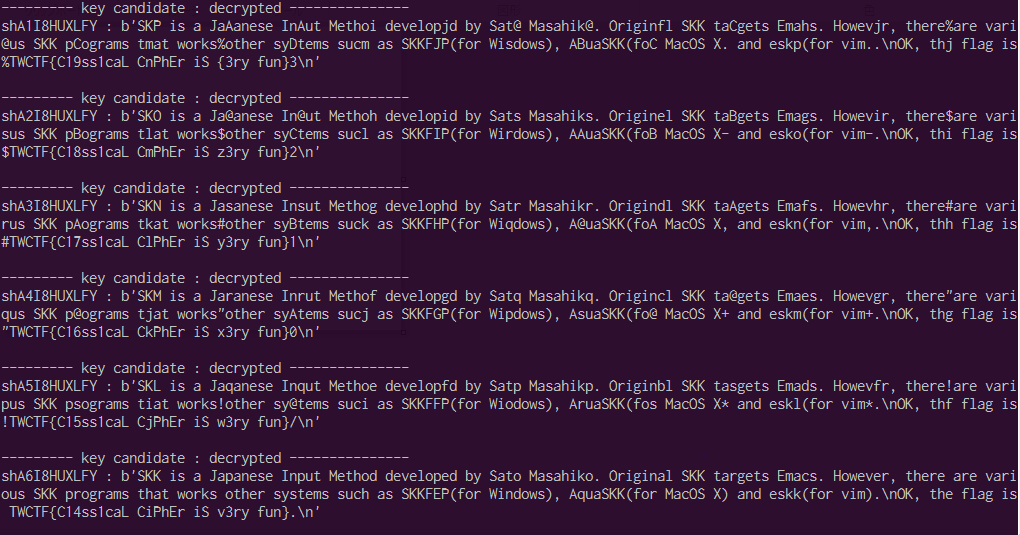
自然に文章を読むことができるのは,鍵が”shA6I8HUXLFY”の時のみです.
TWCTF{C14ss1caL CiPhEr iS v3ry fun}
まとめ
今回の問題のポイントは
- ヴィジュネル暗号とBase64を組み合わせていたことにより,本来ならできない鍵推定手法が使えたこと
です.そして解読手順は以下になります.
- (暗号文が十分に長いヴィジュネル暗号なので)カシスキー・テストにより鍵長を推測する
- 推測した鍵長を4文字1ブロックとして分割し,それぞれのブロックについて総当たり
余談
記事に”推測”と”推定”という二つの言葉が出てきますが,意味に大きな違いはありません.何となく文字列の”長さ”なので測るの方の推測,長さとかではなく絶対的な値を予想するので推定と使い分けています.調べても”推測”と”推定”の明確な違いはよく判らなかったのですが,自分は何となくこう使い分けています.
今回のcipher.pyはPython3を利用していました.そのdecrypt処理を流用したので,自分で書いた部分もPython3です.printの書き方間違えたり,xrange使おうとしたり,間違えて実行するときにpython2系で実行してしまって変な挙動になったりと色々パニクってましたw
参考
- うさぎ小屋 Tokyo Westerns/MMA CTF 2nd 2016: Vigenere Cipher
- その他,記事内で引用させていただいたサイト様